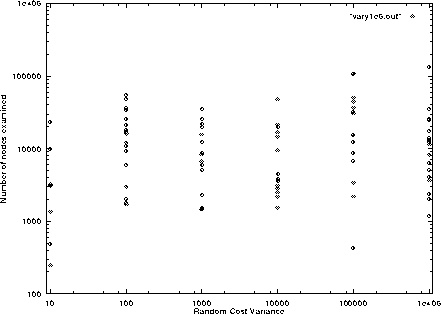
One aspect of the input instance that I suspected to effect the speed of the program is the variance. I created input instances randomly and varied the cost width by what range of random numbers could be picked. For instance if I let the task times be picked randomly between 1 and 10, the variance would be small while, if I let the task times be picked randomly between 1 and 1000000, they tended to have a large variance.

The above plot is based on running my program to schedule 40 tasks and varying the random variance. The vertical measure is the number of nodes examined in the search for the optimum scheduling. As you can see there is little if any difference of running time between the variances. I had reason to believe that the less varied instances perform better is because the lower bound function might be a better bound with these conditions. rank's technique of distributing the tasks as evenly as possible with the given schedule creates pseudo-schedules similar to what a real schedule of little varied costs would be. The better the bounding functions the more nodes that can be ignored. Also from my experience with backtracking I though that the running time might be related to the variance, where there was an inverse relationship. But clearly you can see from the plot that there is no speedup involved.
One thing I did learn from the above experiment is that a task list with zero variance, that is where all task costs are the same, the algorithm correctly gives the optimized schedule from looking at one node. This comes from a perfect initial guess and the good lower bound function. I try three different initial guesses and use the lowest guess from the three, as it turns out one of the guessing algorithms gives the optimal schedule with this condition.