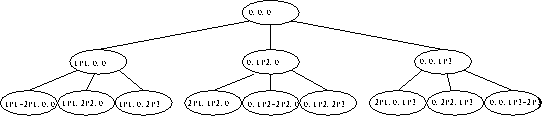
My next algorithm traversed a stored tree that contained all the possible orderings of the tasks at its leaves. Each node in the tree contained three sums of time taken on the three processors. The tree is built with a recursive function that adds the task it is currently on to three new nodes on the tree and calls itself three times for the nodes it has just made. The function stops when it has added the last task. Below is a visual description of the tree:

This is what a tree would look like containing all the orderings of 2 tasks. In the nodes there are some thing like iPj, that is the time for task i on processor j, you can see that the leaves of the tree contain all the possible orderings. Below is pseudo-code to build the tree and traverse it for the smallest ordering:
buildtree(thisnode, taskon)
(new node with taskon on processor 1)
(new node with taskon on processor 2)
(new node with taskon on processor 3)
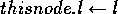
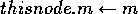
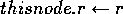
inc(taskon) do
if (
)
buildtree(l, taskon)
buildtree(r, taskon)
buildtree(m, taskon)
findleast(tasktree)if (tasktree.l=NULL) do
if tasktree<lowest do

else
findleast(tasktree.l)
findleast(tasktree.m)
findleast(tasktree.r)
With these two algorithms it is easy to build and search the tree for the smallest ordering. This algorithm has a problem in that it does not store the ordering that was the least, which will be solved in the next algorithm.